Verbindingen in kaart brengen bij je volgende adres. unclibraries_commons
Laten we zeggen dat je je volgende feest plant en piekert over de gastenlijst. Aan wie zou je uitnodigingen moeten sturen? Welke combinatie van vrienden en vreemden is de juiste mix?
Het blijkt dat wiskundigen al bijna een eeuw aan een versie van dit probleem werken. Afhankelijk van wat je wilt, kan het antwoord ingewikkeld zijn.
Ons boek, "De fascinerende wereld van grafiektheorie, "Onderzoekt puzzels als deze en laat zien hoe ze kunnen worden opgelost door middel van grafieken. Een vraag als deze lijkt misschien klein, maar het is een mooie demonstratie van hoe grafieken kunnen worden gebruikt om wiskundige problemen op te lossen op uiteenlopende gebieden als de wetenschappen, de communicatie en de samenleving.
Een puzzel is geboren
Hoewel het bekend is dat Harvard een van de beste academische universiteiten van het land is, zou het je kunnen verbazen dat er een tijd was dat Harvard een van de beste voetbalteams van het land was. Maar in 1931, onder leiding van All-Amerikaanse quarterback Barry Wood, zo was het geval.
Dat seizoen speelde Harvard Army. Halverwege, onverwacht, leidde het leger Harvard 13-0. Klaarblijkelijk boos, vertelde de president van Harvard de legeroverste voor cadetten dat, terwijl het leger misschien beter is dan Harvard in het voetbal, Harvard superieur was in een meer geleerde competitie.
Hoewel Harvard terugkwam om Army 14-13 te verslaan, accepteerde de commandant de uitdaging om te concurreren met Harvard in iets meer geleerde. Er werd overeengekomen dat de twee zouden concurreren - in de wiskunde. Dit leidde ertoe dat het leger en Harvard wiskundeteams selecteerden; de showdown vond plaats in West Point in 1933. Tot Harvard's verbazing won het leger.
De Harvard-Army competitie leidde uiteindelijk tot een jaarlijkse wiskunde competitie voor studenten in 1938, genaamd de Putnam-examen, genoemd naar William Lowell Putnam, een familielid van de president van Harvard. Dit examen was bedoeld om een gezonde rivaliteit in de wiskunde in de Verenigde Staten en Canada te stimuleren. In de loop van de jaren en tot op de dag van vandaag heeft dit examen veel interessante en vaak uitdagende problemen opgeleverd, waaronder degene die we hierboven beschrijven.
Rode en blauwe lijnen
Het 1953-examen bevat het volgende probleem (een beetje anders geformuleerd): er zijn zes punten in het vlak. Elk punt is verbonden met elk ander punt door een lijn die blauw of rood is. Laat zien dat er drie van deze punten zijn waartussen alleen lijnen van dezelfde kleur worden getekend.
Als er in wiskunde een verzameling punten is met lijnen tussen enkele paren punten, wordt die structuur een grafiek genoemd. De studie van deze grafieken wordt grafentheorie genoemd. In de grafentheorie worden de punten echter hoekpunten genoemd en worden de lijnen randen genoemd.
Grafieken kunnen worden gebruikt om een breed scala aan situaties weer te geven. Bijvoorbeeld, in dit Putnam-probleem kan een punt een persoon vertegenwoordigen, een rode lijn kan betekenen dat de mensen vrienden zijn en een blauwe lijn betekent dat ze vreemden zijn.
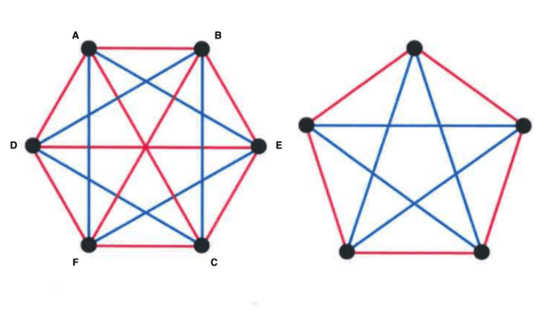
Laat zien dat er drie punten verbonden zijn door lijnen van dezelfde kleur. Gary Chartrand
Laten we bijvoorbeeld de punten A, B, C, D, E, F noemen en een van hen selecteren, zeg A. Van de vijf lijnen die van A naar de andere vijf punten worden getrokken, moeten er drie lijnen van dezelfde kleur zijn.
Zeg dat de regels van A naar B, C en D allemaal rood zijn. Als een lijn tussen twee van B, C, D rood is, zijn er drie punten met alleen rode lijnen ertussen. Als er geen lijn tussen twee van B, C, D rood is, zijn ze allemaal blauw.
Wat als er maar vijf punten waren? Er zijn misschien niet drie punten waar alle lijnen daartussen hetzelfde gekleurd zijn. De lijnen A-B, B-C, C-D, D-E, E-A kunnen bijvoorbeeld rood zijn, de andere blauw.
Van wat we toen zagen, is het kleinst mogelijke aantal mensen dat kan worden uitgenodigd voor een feest (waarbij elke twee mensen vrienden of vreemden zijn) zodanig dat er drie gemeenschappelijke vrienden of drie wederzijdse vreemden zijn zes.
Wat als we zouden willen dat vier mensen gemeenschappelijke vrienden of wederzijdse vreemden zouden zijn? Wat is het kleinste aantal mensen dat we voor een feest moeten uitnodigen om hier zeker van te zijn? Deze vraag is beantwoord. Het is 18.
Wat als we zouden willen dat vijf mensen gemeenschappelijke vrienden of wederzijdse vreemden zouden zijn? In deze situatie is het kleinste aantal mensen dat moet worden uitgenodigd voor een feest om hiervan te worden verzekerd - onbekend. Niemand weet het. Hoewel dit probleem gemakkelijk te beschrijven is en misschien vrij eenvoudig klinkt, is het notoir moeilijk.
Ramsey-nummers
Wat we hebben besproken, is een soort getal in de grafentheorie, een Ramsey-getal. Deze nummers zijn genoemd naar de Britse filosoof, econoom en wiskundige Frank Plumpton Ramsey.
Ramsey stierf op de leeftijd van 26 maar behaalde al op zeer jonge leeftijd een zeer curieuze stelling in de wiskunde, die hier onze vraag opriep. Stel dat we een ander vliegtuig hebben vol punten verbonden door rode en blauwe lijnen. We kiezen twee positieve gehele getallen, genaamd r en s. We willen exact r-punten hebben waarbij alle lijnen daartussen rood zijn of s punten waar alle lijnen daartussen blauw zijn. Wat is het kleinste aantal punten waarmee we dit kunnen doen? Dat heet een Ramsey-nummer.
Stel bijvoorbeeld dat we willen dat ons vliegtuig ten minste drie punten heeft, verbonden door alle rode lijnen en drie punten verbonden door alle blauwe lijnen. Het Ramsey-nummer - het kleinste aantal punten dat we nodig hebben om dit mogelijk te maken - is zes.
Wanneer wiskundigen naar een probleem kijken, stellen ze zichzelf vaak de vraag: suggereert dit een andere vraag? Dit is wat er is gebeurd met Ramsey-nummers - en feestproblemen.
Hier is er bijvoorbeeld een: vijf meiden plannen een feestje. Ze hebben besloten om enkele jongens uit te nodigen voor het feest, of ze de jongens nu kennen of niet. Hoeveel jongens moeten ze uitnodigen om er zeker van te zijn dat er altijd drie jongens onder hen zullen zijn, dat drie van de vijf meisjes vrienden zijn met alle drie de jongens of niet bekend zijn met alle drie de jongens? Het is waarschijnlijk niet eenvoudig om een goede inschatting te maken van het antwoord. Het is 41!
![]() Er zijn maar heel weinig Ramsey-nummers bekend. Dit weerhoudt wiskundigen er echter niet van om dergelijke problemen op te lossen. Vaak kan het niet oplossen van één probleem leiden tot een nog interessanter probleem. Zo is het leven van een wiskundige.
Er zijn maar heel weinig Ramsey-nummers bekend. Dit weerhoudt wiskundigen er echter niet van om dergelijke problemen op te lossen. Vaak kan het niet oplossen van één probleem leiden tot een nog interessanter probleem. Zo is het leven van een wiskundige.
Over de Auteurs
Gary Chartrand, emeritus hoogleraar wiskunde, Western Michigan University; Arthur Benjamin, hoogleraar wiskunde, Harvey Mudd College, en Ping Zhang, hoogleraar wiskunde, Western Michigan University
Dit artikel is oorspronkelijk gepubliceerd op The Conversation. Lees de originele artikel.
Related Books:
at InnerSelf Market en Amazon